Analysing semantic associations in VGI data

Volunteered Geographic Information (VGI) such as OpenStreetMap (OSM) can be a rich resource for many applications. Therefor VGI-projects have to mitigate between the requirements of the the volunteers and the machines. On the one hand, the data format should be simple and general in order to make contributing to the project easy for the volunteers. On the other hand, processing the data with machines benefits from rich data structures with formally defined meanings. Unfortunately it is difficult to serve both purposes at the same time. Researchers at HeiGIT bridge the gap between volunteers and machines by teaching machines to find semantic associations in VGI data.

For instance, OSM captures the meaning of its data with key-value-pairs. Given the key “building” and the value “residential” we can form the key-value-pair “building=residential” denoting that the data element represents a building of type residential. For us humans, this simple structure is easy to understand. It is obvious that “addr:housenumber=45” and “addr:street=Berliner Straße” are parts of an address because we know much about how addresses are composed from smaller parts. But how does the machine know that housenumbers and streets are related?

To teach the machine about such relations, we employ a technique called association rule learning. By analyzing which keys occur together frequently, we can derive association rules such as “addr:housenumber ⇒ addr:street”. This rule means that, typically, objects annotated with a housenumber are also annotated with a street. Hence, the machine is able to infer an association between the two keys from the frequency of their cooccurrence.

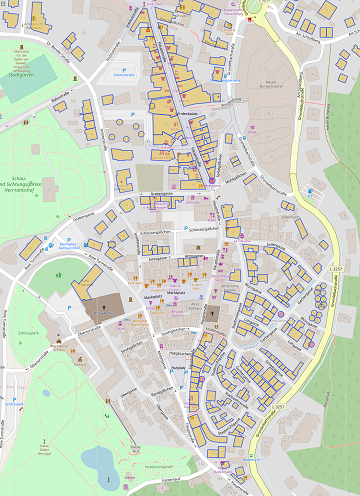
When thinking about data quality, the exceptions to such a rule are even more interesting than the rules themselves. For example, we found many exceptions to the above rule in the town of Weinheim as highlighted in the figure. While single exceptions may be due to errors in the data, there is probably a systematic reason for the exceptions in this case. In particular, it is important that applications know about such systematic differences. For example, a geocoder that maps addresses to geographic coordinates on the Earth’s surface must know that the addresses are annotated differently in Weinheim.