The ohsome region of the month blog post series is back and since it’s summer this time we’re taking you to the coast. Before that happens, if this is your first blog post of this format you might want to take a look at former blog posts of this series for example one on railway networks or our last blog post on building information. Now that this is out of the way, let’s get started, shall we?
Data:
As usual, our boundary-data comes from here. For this month’s analysis we chose to look at the following countries as well as which of them has the longest tagged coastline:
- USA
- Canada
- UK
- Russia
- Chile
- Madagascar
- India
- Australia
- Norway
Requests:
After choosing the countries you want to look at, you’ll have to decide on which endpoints and filter-conditions fit the question best. For this we chose the endpoint /elements/length/groupBy/boundary for absolute values and /elements/length/density/groupBy/boundary to compare the length of the coastline with respect to the size of the countries. To make things easier you can find a snippet here with the boundary files as well as a request example which you can use to build your own requests.
Filter conditions:
filter = type:way and natural=coastline
showMetadata = yes (optional)
time = 2021-06-06
Data Exploration:
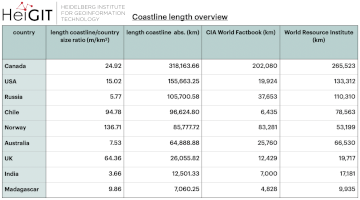
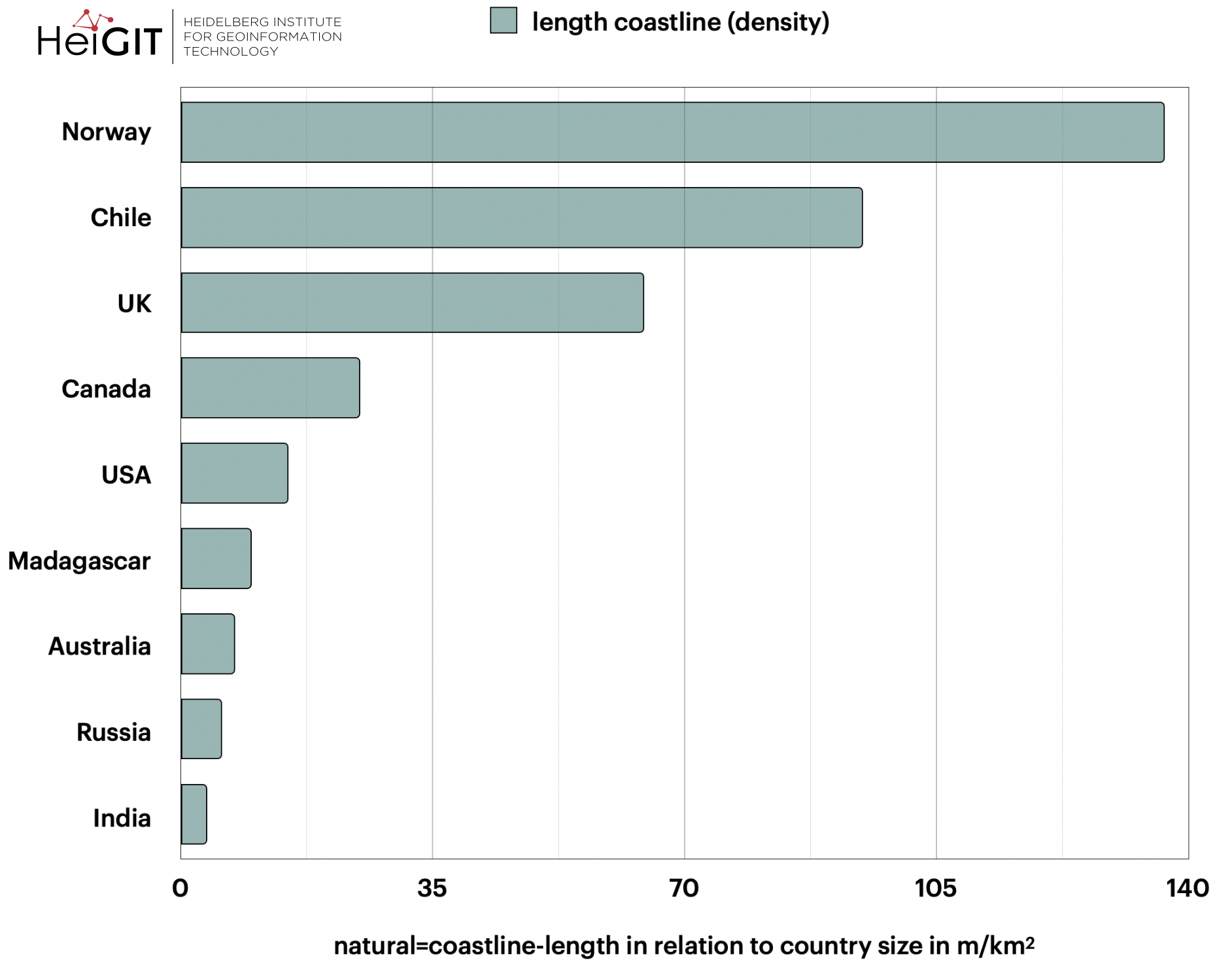
Above you can see two rankings, one for the absolute values (upper graphic) and one for the values in relation to country size (lower graphic). Both of them display the countries sorted by the longest tagged coastline.
As to be expected the rankings show quite different results from each other. For example, you find Canada and the US to have the longest coastlines when setting the focus on absolute values. However when looking at it in relation to the country size Norway and Chile are at the top.
When looking at the density-derived values the ranking looks about right, as the bigger countries all have relatively low values whilst the countries of smaller sizes have much longer coastlines in relation. But as soon as you consider other rankings, especially with respect to absolute values, you’ll notice it’s much more complex. Determining the “one objectively correct length” is complex if not impossible. When looking at other rankings of which coasts are the longest you’ll get different results, which is kind of depending on how detailed the length was calculated. Of course, this is no different with our OSM-derived dataset.
The differences in coastline length compared to the values given by the CIA World Factbook or the World Resource institute (Burke et al. 2001) is due to a phenomenon called the “coastline paradox“. It states how the length of coastlines can be measured by adjusting approximation lines to them, yet with increasing level of detail of the approximation lines the coastline length usually increases too.
So for example:
If the measuring segments are in 100km-steps the coastline tends to get longer but if they are in 250km-steps it tends to get shorter. In addition, the length depends on the scale of the map used due to the amount of detail shown in maps of different scales. While one could assume that you could go into indefinite detail with the approximation lines. But that is not the case as coastlines aren’t something static (e.g. variable water level) and there is a kind of temporal dependency of the accuracy of the length values. This might be the case for erosion and relocation of deposits and the further into detail you go the faster the values are outdated because of these natural variabilities. Therefore, all the following values are merely estimations which themselves depend on the scale of the map used as well as the length of the measure segments. Unfortunately, this information isn’t given for any of the rankings. The true coastline length is highly dynamic and cannot be known precisely.
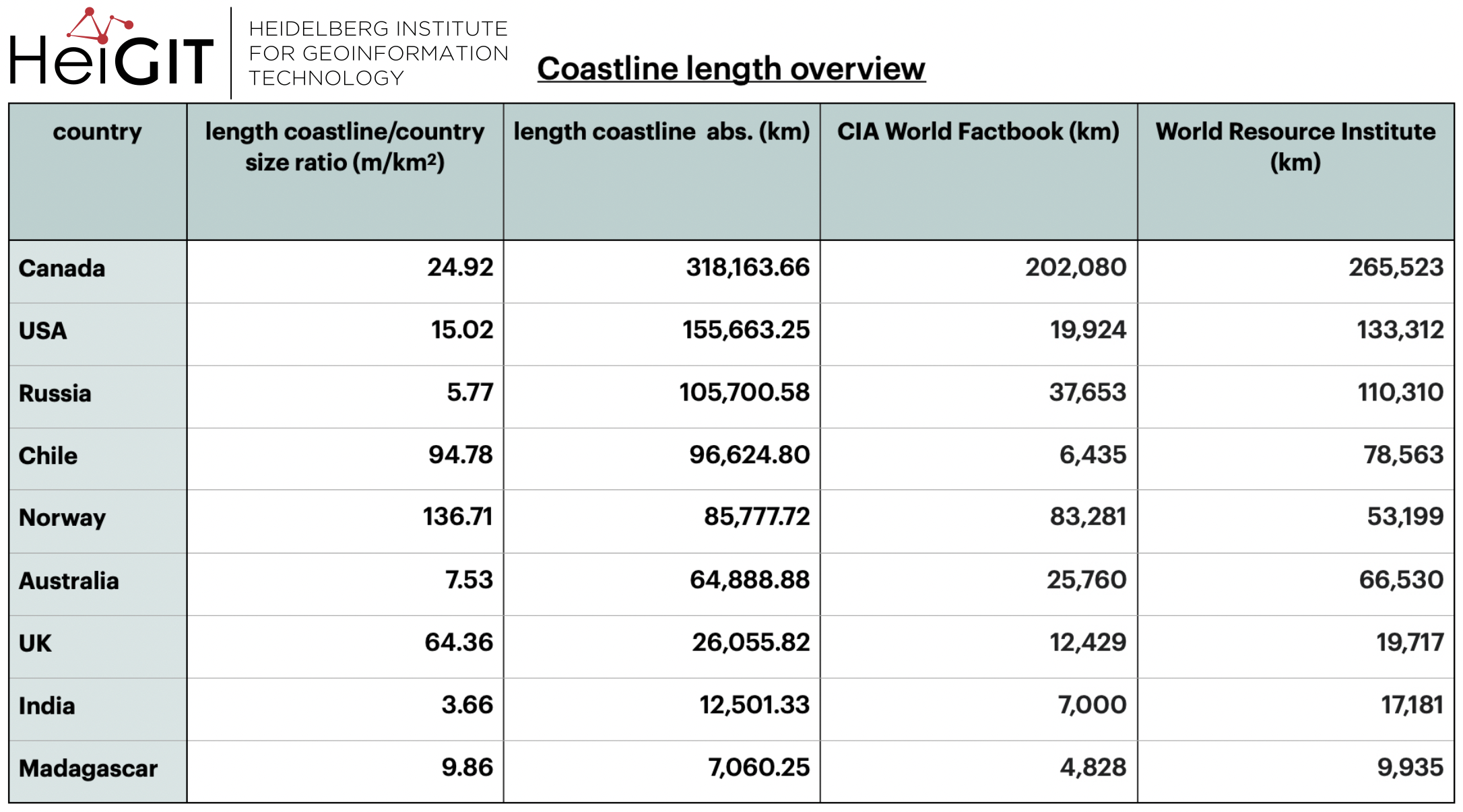
Above you can see a table with our request outputs as well as the values of two other rankings used (WFB & WRI) so you have a comparison
A lot of the values are very different from those presented in the CIA World Factbook where the coastline is described as “the total length of the boundary between the land area (including islands) and the sea”. Most of these values are in fact about twice as long. However, a lot of them seem similar although not equal to the values given by the World Resource Institute (Burke et al. 2001). Norway’s request values are actually closer to the ones given in the World Factbook whilst Canada, the US and the UK all show higher request values than both of the sources. India and Madagascar have request-values that lie in between both rankings. Especially for India, this can’t be due to islands as they are included in the World Factbook values.
Ranking:
As the result of the requests were two rankings with differing outcomes and we have another two sources to orientate when naming our own ohsome region of the month with the longest coastline. To create a final ranking we chose to use a point system. The highest ranking country gets the highest amount of points (in this case 9 points) and the lowest ranking one gets the lowest amount of points (1 point), taking the request values into account. In case there would be two or more regions with the same amount of points, we’ll go a step further and compare the values of the WFB and the WRI rankings and look which region has the highest values.
With that we came out with the subsequent ranking:
- Canada
- Norway
- Chile
- USA
- UK
- Russia
- Australia
- Madagascar
- India
Thanks for reading this ohsome region of the month-blog post, we hope you liked it. Stay tuned for more!
Background info: the aim of the ohsome OpenStreetMap History Data Analytics Platform is to make OpenStreetMap’s full-history data more easily accessible for various kinds of OSM data analytics tasks, such as data quality analysis, on a regional, country-wide, or global scale. The ohsome API is one of its components, providing free and easy access to some of the functionalities of the ohsome platform via HTTP requests. Some intro can be found here:
- ohsome general idea
- ohsome general architecture
- how to become ohsome blog series
- how spatial joins queries work in the OpenStreetMap History Database OSHDB
Burke, L., Kura, Y., Kassem, K., Revenga, C., Spalding, M. & McAllister, D. 2001. Pilot Analysis of Global Ecosystems – Coastal Ecosystems. World Resource Institute. Washington DC. p.14.
Weisstein, Eric W. “Coastline Paradox.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/CoastlineParadox.html